COLOR SEGMENTATION

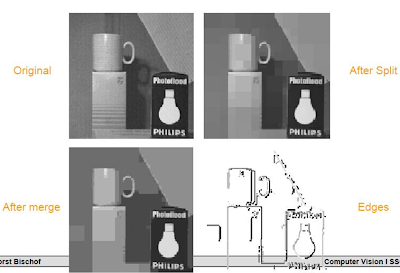
Region Segmentation

REGION MERGING


- a process of eliminating false boundaries and spurious regions by merging adjacent regions that belong to the same object.
- suitable for edge data segmentation.
- involve identifying each pixel in a raw image as a small region and then merging regions together systematically  to grow larger regions.

  ++ Algorithm for Region Merging ++
        1. Merging schemes begin with a partition satisfying condition (4) - using threshold
                                               
                                                       (4) P(Ri) = True

        2. Then proceed to fulfill condition (5) by gradually merging adjacent image regions.
                   
                                                       (5) P(Ri U Rj) = False

           a. Form initial regions in the image.
           b. Build a region adjacency graph (RAG).
           c. For each region do :-  consider its adjacent region and test to see if they are similar.
                                             -  for regions that are similar (P(Ri U Rj) = True), merge them and modify the      
                                                RAG
           d. Repeat step (c) until no regions are merged.

---------------------------------------------------------------------------------

REGION SPLITTING

 - a process of adding missing boundaries by splitting regions that contain parts of different objects.

 ++ Algorithm for Region Splitting ++

       1. Splitting schemes begin with a partition satisfying condition (5)

                                                     (5) P(Ri U Rj) = False

       2. Then, proceed to satisfy condition (4) by gradually splitting image regions.

                                                      (4) P(Ri) = True

             a.  If P(R) = False, split R into four quadrants.
             b. If P is false on any quadrant, subsplit.

---------------------------------------------------------------------------------

REGION SPLITTING AND MERGING

- A better result of region segmentation can be produced by integrating both region splitting and merging together.

- Takes partition that possibly not satisfies neither condition (4) nor (5) with the aim of producing a segmentation that satisfies both condition.

++ Algorithm for Region Splitting and Merging++

   1.  Split into four disjointed quadrants any region Ri where P(Ri) = False.

   2.  Merge any adjacent regions Rj and Rk for which P(Rj U Rk) = True.

   3.  Stop when no further merging or splitting is possible.

---------------------------------------------------------------------------------

REGION USING QUAD TREES
- Extension of pyramids for binary images.
- Three types of nodes (white,black,grey).
-White or black node no splitting.
- Gray node split into 4 sub-regions

---------------------------------------------------------------------------------

           

JPEG vs JPEG 2000

Assalamualaikum. Hello readers, balqis here. This time, I would like to discuss the comparison between JPEG and JPEG 2000. Have you ever heard about JPEG? What is JPEG? JPEG stands for 'Joint Photographic Experts Group'. It is a standard method of compressing photographic images. The file extensions for this format are .JPEG, .JFIF, .JPG, OR .JPE although .JPG is the most common on all platforms. JPEG format enable lossless compression. Example of lossless compression technique are Huffman coding, run-length coding, and many more.

Here, I put some of the jpeg compression implementation code. To implement basic JPEG compression using only basic Matlab functions. .  This included going from a basic grayscale bitmap image all the way to a fully encoded file readable by standard image readers.

Step1:  Converting the base image to 8x8 matrices, DCT transform, quantizing
Step 2:  Zig-Zag Encoding of Quantized Matrices.
Step 3:  Conversion of quantized vectors into the JPEG defined bitstream
Step 4:  Construction of the JPEG File header, Writing the File

Lets try this :)

You must wonder, what is Huffman coding right? Emm, Huffman code, developed by D. Huffman in 1952, is a popular technique for removing coding redundancy. The result after Huffman coding is variable length code, where the code words are unequal length. Lets see, the Huffman example :)

Then, JPEG 2000 was introduced. But why they introduce JPEG 2000 and what is the difference between JPEG  and JPEG 2000?   Ok, let me explain it one by one. To be able to manipulate more and more data, image compression must not only reduce the necessary storage and bandwidth requirements, but also allow extraction for editing, processing, and targeting particular devices and applications.

The JPEG-2000 image compression system has a rate-distortion advantage over the original JPEG. More importantly, it also allows extraction of different resolutions, pixel fidelities, regions of interest, components, and more, all from a single compressed bitstream.

To be shortened, let me list the advantages of JPEG 2000 over JPEG :)

• JPEG 2000 advantage is it offers both lossy and lossless compression at the same time while JPEG usually utilize lossless compression.
• JPEG 2000 format includes much richer content than existing JPEG files.
• JPEG 2000 can display an image at different resolution and size from the same image file.

Below is the differences of JPEG and JPEG 2000. Can you spot the differences? 

That's a little bit explanation about JPEG and JPEG 2000. Don't forget to read our previous post by Raihan entitled Image Enhancement. Have a nice day.

References:

1. http://www.verypdf.com/pdfinfoeditor/jpeg-jpeg-2000-comparison.htm
2. http://www.photozone.de/jpeg2000-vs-jpeg-vs-tiff
3. http://ce.sharif.ac.ir/courses/84-85/2/ce342/resources/root/Lecture%20Notes/dcc2000_jpeg2000_note.pdf

Image Enhancement

Hello readers... this week we are back with new topic in Image Processing which is: Image Processing in Spatial Domain and Frequency Domain.

Why we need to enhance image???
It is because  it improves the interpret-ability or perception of information in images for human viewers. It is also providing better input for other automated image processing techniques

Now, let's take a look about what it is all about with these two different domains..

Spatial Domain	Frequency Domain
2D function f(x,y) represents pixel values	2D function f(x,y) represents frequency values
Techniques that operate directly on pixels	Techniques are based on modifying the Fourier Transform (FT) of an image.
The computational cost of filtering depends on filter size	Cost-filtering is fixed (not-dependant on size of the equivalent spatial domain convolution filter)
Changes in pixel positions correspond to changes in scene.	Changes in image position correspond to changes into spatial frequency
General model: g(x,y) = h(x,y) * f(x,y) + n(x,y) g(x,y) = Degraded image h(x,y) = Degradation function f(x,y) = Original image n(x,y) = Additive noise function	General model: G(u,v) = H(u,v) *F(u,v) + N(u,v) G(u,v) = FT of degraded image H(u,v) = FT of degradation function F(u,v) = FT of original image N(u,v) = FT of noise function

Do you ever know how to determine the frequency of one particular image???
What do frequencies mean in an image ??

Lab 3.2 - Spatial Filtering

Hye there.. it's Aan again...do u still remember previous post by my course-mate, Balqis about INTENSITY TRANSFORMATION ?? feel free to click here if u missed it..since it has slight relation with this post topic, i recommend u to go through the intensity transformation first.

Now, I would like to share about Spatial Filtering..

Spatial Filtering can be used to smooth, blur, sharpen, or find the edges of an image. It is also known as neighbourhood processing.

Lets try on how to do average filter that apply at location 2,2
This 2,2 location is referred to the pixel of the image

the original image of stock_cut

stock_cut after being filtered

The following table, modified from page 94 of Digital Image Processing, Using MATLAB by Rafael C. Gonzalez, Richard E. Woods, and Steven L.Eddins, summarizes the additional options available with imfilter function.

The imfilter function which applied on stock_cut image above have inherent problem when working with corners and edges. the problem is that some of the "neigbours" are missing. 

the solutions for this problem are : ZERO-PADDING and REPLICATING

Lets try these 'zero-padding' and 'replicating' on cat image.

Note that the filter used below is a 5x5 averaging filter which can be carry out using this syntax:

Next, read the image to be filtered by using this command.

original image of 'cat.jpg'

Below are the command function to do zero-padding, replicate, symmetric, and circular to an image

The results of filtering are shown as below:

The disadvantage of zero-padding is that it leaves dark artifacts around the edges of the filtered image (with white background). You can see this as a dark border along the bottom and right-hand edge in the zero-padded image above.

Ok, lets move to next sub-topic : Filtering Mode (Correlation vs Convolution)

Convolution rotates the filter by 180 degrees before performing multiplication. Diagram below demonstrates the two operations for position 3,3 of the image:

The following are example codes to demonstrate Correlation and Convolution on 'cat.jpg' image:

Next, we will go through on Size Options in imfilter process.

The two size options are 'FULL' and 'SAME'. The 'full' will be as large as the padded image, whereas the 'same' will be the same size as the input image.

Below are MATLAB syntax  on how to create a 'full' and 'same' image:

Last but not least, we can also create SPECIAL FILTERS by using a fspecial function which requires an argument that specifies the kind of desired filter.

The following examples will show you three filters created by fspecial and the results of 'cat.jpg' image:

Alright...that's all for Spatial Filtering lesson. Hope this will help.. Feel free to give any comment below :)

Keep following our update.. Thanks for reading... Bye 

LAB 3: INTENSITY TRANSFORMATION (MATLAB)

assalamualaikum to our fellow lecturer and friends. have you ever heard about intensity transformation and spatial filtering? this week, we have learned something new about matlab which are intensity transformation and spatial filtering. there are four main function of intensity transformation:

• photographic negative (using imcomplement)
• gamma transformation (using imadjust)
• logaritmic transformation (using c*log(1+f))
• contrast-stretching transformations (using 1./(1+(m./(double(f)+eps)).^E)

photographic negative (using imcomplement) 

then what is photographic negative? ok, in the easiest words, it means that the true black becomes true white and vise versa. matlab has a function to create this photographic negative by imcomplement (f). lets see our coding example that we have done during lab session :)

>>   I=imread('cat.JPG')

>>  J=imcomplement(I);

>>  imshow(I)

>>  figure, imshow(J)

original image

after photographic negative

gamma tranformation (using imadjust)

next is about gamma transformations. what is gamma transformation? with gamma transformation, we can curve the grayscale components either to brighten the intensity or to darken the instensity. when the component grayscale darken, it means the gamma is less than one and vice versa. lets see the coding example of gamma transformation :)

>>   I = imread('tire.tif');

>>   J=imadjust(I,[],[],1);

>>   J2=imadjust(I,[],[],3);

>>   J3=imadjust(I,[],[],0.4);

>>   imshow(J);

>>   figure, imshow (J2);

>>   figure, imshow (J3);

J

J2

J3

logaritmic transformations (using c*log(1+f))

usually, logarithmic transformation used to brighten the intensities of an image of lower intensity values. its function in matlab can be shown as,    g = c*log(1+double(f)) . here, we paste some matlab code example  for logaritmic transformation :)

>>   I = imread('tire.tif');

>>   I2=im2double(I);

>>   J=1*log(1+I2);

>>   J2=2*log(1+I2); 

>>   J3=5*log(1+I2); 

>>   imshow(I) 

>>   figure, imshow(J)

>>   figure, imshow(J2)

>>   figure, imshow(J3)

original image

J

J2

J3

contrast-stretching transformations (using 1./(1+(m./(double(f)+eps)).^E) 

this is the last part of intensity transformation for our lab. what is contrast-stretching transformation? urm, contrast-stretching transformation results in increasing the contrast between the darks and the lights. this will end up the dark being darker and the lights being lighter, with only few levels of gray in between. lets see our coding example and screenshot in plot form to enable readers to make contrast comparison easily :)

a)  light to lighter

>> I = imread('tire.tif');

>> I2=im2double(I);

>> m=mean2(I2)

>> contrast1=1./(1+(m./(I2+eps)).^4);

>> contrast2=1./(1+(m./(I2+eps)).^5);

>> contrast3=1./(1+(m./(I2+eps)).^10);

>> figure(1), subplot(2,2,1),imshow(I2),xlabel('I2')

>> figure(1), subplot(2,2,2),imshow(contrast1),xlabel('contrast 1')

>> figure(1), subplot(2,2,3),imshow(contrast2),xlabel('contrast 2')

>> figure(1), subplot(2,2,4),imshow(contrast3),xlabel('contrast 3')

(a) contrast-stretching transformation. bright to brighter. 

a)  dark to darker

>> I = imread ('tire.tif');

>> I2=im2double(I);

>> contrast1 = 1./(1+(0.2./(I2+eps)).^4);

>> contrast2 = 1./(1+(0.5./(I2+eps)).^4);

>> contrast3 = 1./(1+(0.7./(I2+eps)).^4);

>>figure(1), subplot(2,2,1), imshow(I2), xlabel('I2')

>>figure(1), subplot(2,2,2), imshow(contrast1), xlabel('contrast1')

>>figure(1), subplot(2,2,3), imshow(contrast2), xlabel('contrast2')

>>figure(1), subplot(2,2,4), imshow(contrast3), xlabel('contrast3')

(b) contrast-stretching transformation. dark to darker. 

we hope our post on this time will help you to understand a little bit about intensity transformation. in the next post, we will update about the spatial filtering in matlab. thanks you :)